Noether’s Theorem, Symmetries, and Invariant Neural Networks
When I tell physicists that I am working on invariant and equivariant neural network architectures which exploit symmetries, they often mention Noether’s theorem. In this post, I am trying to answer the question of how the two topics are connected. I will first give some background for Noether’s theorem, including a short intro to Lagrangian and Hamiltonian mechanics. Then, we will analyse the connection to equivariant & invariant neural networks. I divide this connection into two subsections: (1) physics-inspired neural networks that make use of the Lagrangian or Hamiltonian directly and (2) the general topic of invariance, equivariance and symmetries in neural networks.
This is a brief blog post aimed especially at people who have never worked with Lagrangian or Hamiltonian Neural Networks before – just like myself. I added some links for further reading at the bottom.
Lagrangian Dynamics and Noether’s Theorem
In classical mechanics, to understand the dynamics of a physical system, one simple approach is to write down all relevant forces of the system as well as the equations for momentum and energy conservation. For simple systems, this is a straight forward recipe for obtaining the equations of motion, i.e. determining how the system evolves over time. In other words, obtaining the true path. However, even for some seemingly minimalistic systems like the double pendulum, it is almost impossible to solve these equations of motion.
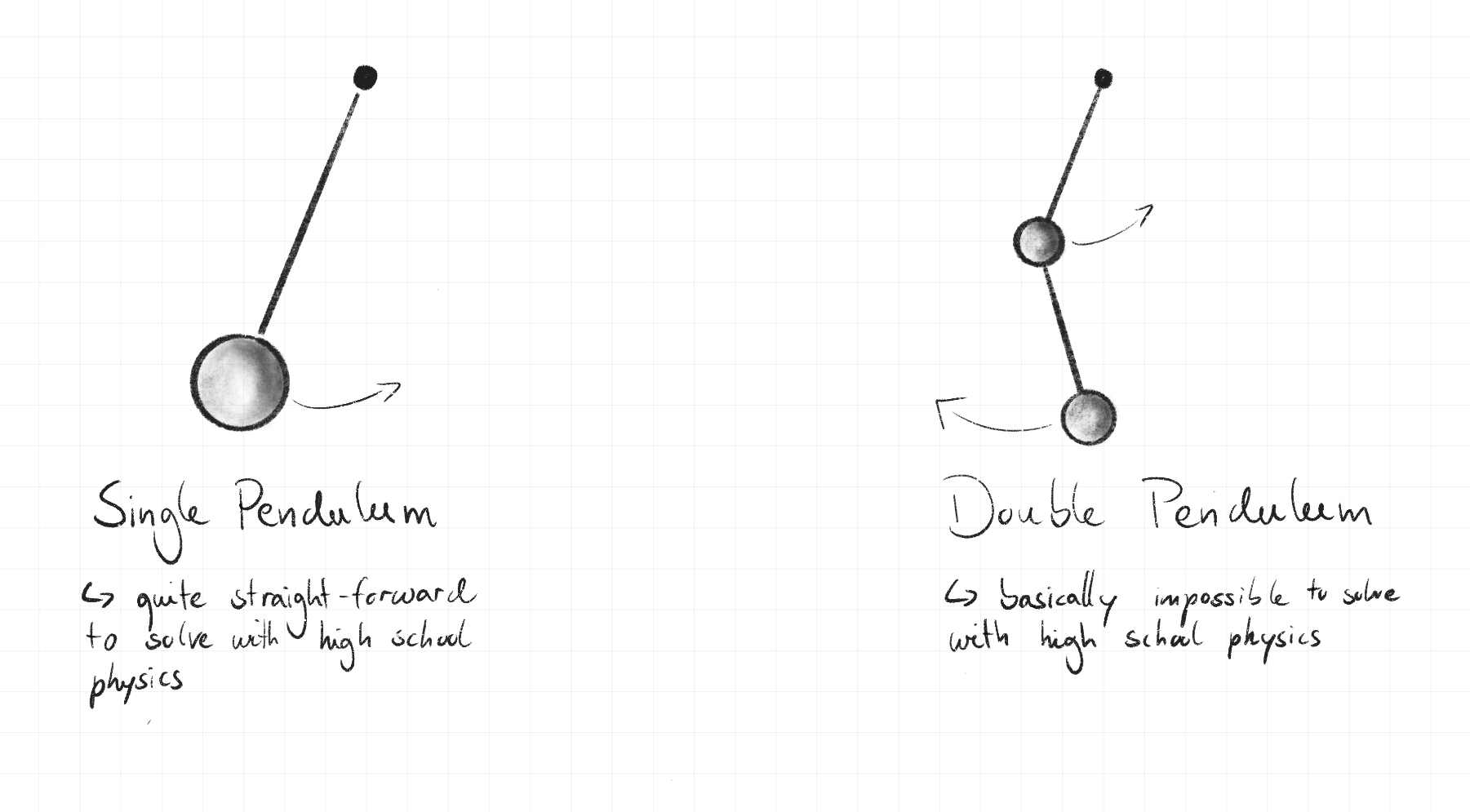
An alternative approach is Lagrangian Dynamics, which reframes the dynamical problem in terms of a set of generalised coordinates that completely characterise the possible motions of the particle. The formulation implicitly exploits the constraints in the system, such as the lengths of the pendulums, which allows us to find the true path of the system (in this case, how the pendulums move over time) more easily.
To use Lagrangian dynamics, we first need to construct the Lagrangian $L$, which is defined as the difference between the kinetic energy ($T$) and the potential energy ($U$) of the system:
\[L = T - U.\]The integral of $L$ over time is called the action. The true path of the system minimises this this integral, which is known as the principle of least action. It directly follows that the action cannot change under small varations of the path. Mathematically, this can be shown to be equivalent to the following condition:
\[\frac{\partial L}{\partial x} - \frac{d}{dt} \frac{\partial L}{\partial \dot{x}} = 0,\]which connects the derivatives of the Lagrangian with respect to location, time, and generalised momentum. This equation is known as the Euler-Lagrange equation.
One advantage of Lagrangian dynamics is its flexibility with respect to what (generalised) coordinates to use, cleverly exploiting the constraints of the system (in this case, the lengths of the pendulums). Concretely, using angles instead of 2D coordinates for writing down $T$ und $U$ is a big help. Instead of having four coordinates ($x_1, y_1, x_2, y_2$) to describe the positions of the circles at each time, we just have two angles.
So what does Noether have to do with the Langrangian and the Euler-Lagrange equation? Noether discovered that any continuous symmetry of $L$ is connected to a conserved quantity of the system. For example, if $L$ does not change under translation (i.e., has a translational symmetry), then momentum is conserved. If $L$ does not change under shifts in time, energy is conserved. This was a major discovery and has had a strong impact on our understanding of physics ever since, putting a bigger emphasis on symmetries and invariances. (Bronstein et al.)
Similar, but Different: the Hamiltonian
We learned that the Lagrangian is defined as the difference betwee kinetic and potential energy. This has a striking similarity to another physical quantity that comes up in machine learning these days, the Hamiltonian:
\[H = T + U\]Just as for the Lagrangian, there are equations for the Hamiltonian that define the dynamics of the system:
\[\dot{q}_{i}=\frac{\partial H}{\partial p_{i}} \quad \quad \dot{p}_{i}=-\frac{\partial H}{\partial q_{i}}\]Given how similar the two formulations look, what’s the difference between the two? One difference is that the Hamiltonian uses the momentum $p_{i}$ whereas the Lagrangian just uses the time derivative of the position $\dot{x}$. If we only care about simple particle systems, then all we need to do to get the momentum is multiply $\dot{x}$ with the mass. In more complicated systems, e.g., when considering magnetic fields or effects from special relativity, this can become an issue. In those cases, the momentum is not local anymore and can be very challenging and/or time consuming to compute.
Neural Networks using the Hamiltonian or the Lagrangian
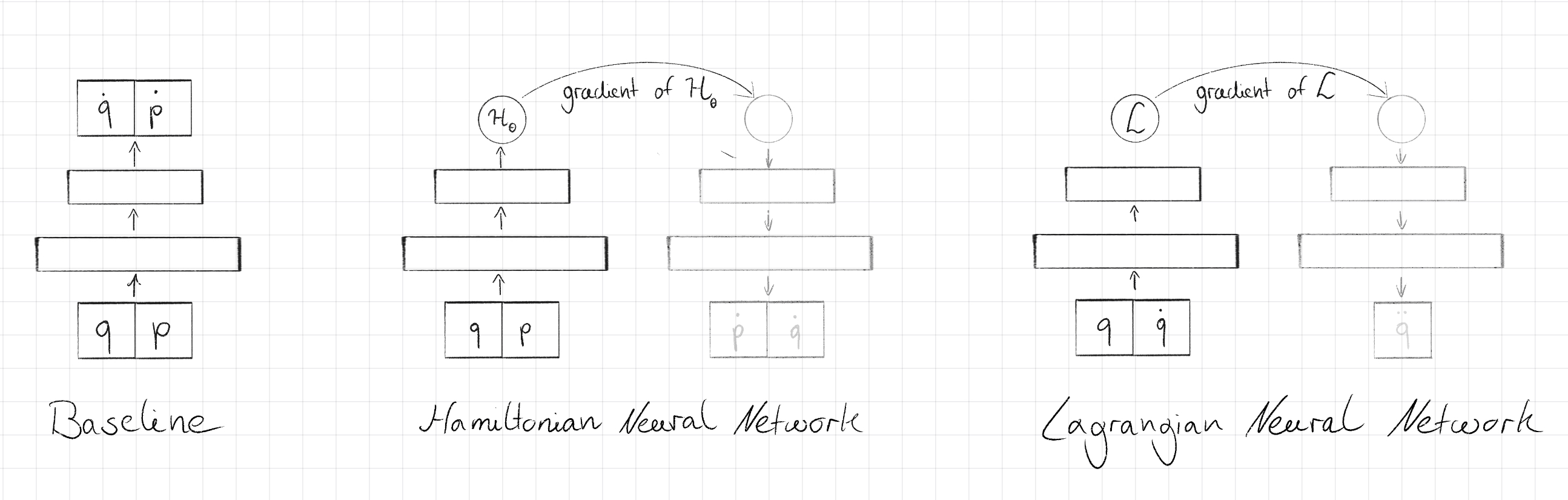
One way to understand a physical system is to compute the forward dynamics, i.e. to predict the next state given the current state and integrate over time, e.g., using the Euler or the Leapfrog method. A simple neural network approach could be to take the coordinates and the velocities and predict the acceleration. Hamiltonian Neural Networks (HNNs) and Lagrangian Neural Networks (LNNs) provide an alternative: the neural network predicts a scalar quantitiy, the Hamiltonian and the Lagrangian, respectively. As neural networks are differentiable (they need to be for backprop to work), the position and velocity updates can be computed by calculating the derivative. Crucially, the dynamics equations (the Euler-Lagrange equation in the case of LNNs) conserve energy over time, hence this symmetry is baked into the neural network. The authors of both papers experimentally show this advantage over the naive baseline described above.
Interestingly, one does not always want to conserve energy, for example in the presence of (potentially time dependent) external forces and energy dissipation. Desai et al. address these shortcomings of the approaches described above in their work on Port-Hamiltonian Neural Networks. Disclaimer: this is very much an active and growing field with many great papers that are not covered here (mainly because I am not an expert in this field). The purpose of this sub-section is just to give a superficial idea of how the concepts above can be used in machine learning.
The Connection to General Symmetries in Machine Learning
The approaches described above are great when we want to understand the dynamics of physical systems with multiple particles. However, most machine learning tasks cannot be naturally framed in this way. This doesn’t mean that those tasks don’t have symmetries and conserved quantities. Hence, I asked myself the question whether general symmetries in machine learning tasks are connected to Noether’s theorem.
I once caught myself saying “Noether connected symmetry and invariance” – but that would trivialise her brilliance. Most definitions of symmetry already make a connection to invariance. E.g., in machine learning, Mallat defines a task symmetry as a property of a ground truth function $f(x)$ that the neural network is trying to learn. If the actions of a symmetry group applied to $x$ do not change the output $f(x)$, then the function $f$ is symmetric with respect to this group. In other words, this function is invariant. Analogously, in Noether’s theorem, the Lagrangian $L$ is invariant with respect to, e.g., translations. The special bit, however, is that this symmetry/invariance of $L$ is connected to a fundamental, conserved property, such as energy or momentum. I am not aware of any such ‘fundamental’ conserved properties in machine learning. However, there is maybe one parallel: in machine learning, noticing the symmetry of $f$ is not helpful in itself, it’s just an observation. Cool things start to happen when connecting the symmetry/invariance of the ground truth function to the invariance of other quantities, such as the loss function. And how do we get a loss function that is invariant with respect to some symmetry transformations? – We use equivariant and invariant network layers.
Further Reading I highly recommend watching Miles Cranmer’s presentation of Lagrangian Neural Networks and Bronstein’s ICLR keynote about geometric deep learning, which also draws the link between Noether and symmetries in machine learning. There are also many related papers that I hope to have the time to read, including: Neural Mechanics: Symmetry and Broken Conservation Laws in Deep Learning Dynamics (ICLR 2021). It examines how symmetries of the loss functions are connected to the gradients and comes with a with blog post and seminar talk. There is also a follow-up arXiv paper from May this year: Noether’s Learning Dynamics: The Role of Kinetic Symmetry Breaking in Deep Learning. Also, Shubhendu Trivedi pointed out this recent arXiv paper, which sounds excellent.
Thank you to Adam, Bradley, Stefan, and Wolfram for insightful conversations about this topic!