Colliding Circles Toy Datasets
We created these datasets for studying relational reasoning in the context of multi-object tracking. Find the paper here. I find these datasets both interesting and fun - hence my decision to dedicate an extra page for them. Let me know if you have any questions about using them.
Physics-inspired toy examples are a widespread tool in machine learning to test a model’s efficacy in a targeted, interpretale way. Moving circles in a two-dimensional box are a particularly popular instance of this due to their simplicity and flexibility (Visual Interactions Networks, Relational Neural Expectation Maximization). Previous works in this domain have often been using elastic collisions without long-range interactions or planetery systems (all particles attract each other).
Our goal was to create a dataset which tests the relational-reasoning capabilities of an (end-to-end) multi-object tracker (such as MOHART).
We evaluated the tracker as follows (but feel free to train/test your model differently): In the first time step, the ground truth bounding boxes of all objects are provided to the algorithm. The following frames are subsequently shown to the algorithm. For each time step the model is supposed to predict the bounding boxes either of the current time step or a future time step. The former is known as Visual Object Tracking (VOT). The latter mode turns the tracking task into a short-horizon prediction task. This proved to be a better test of the model’s relational reasoning capabilities as tracking can often be solved perfectly without awareness of other objects (except in cases like occlusion).
Colliding Circles
All circles collide with each other. Each particle is propagated according to its 2D velocity vector. Each collision conserves both momentum and energy. The boundaries are elastic walls. The red boxes indicate the ground truth bounding boxes provided with the data.
Introducing Occlusions
To increase the difficulty of the dataset, we introduce occlusions. Circles of the same size collide with each other while as circles of different sizes pass through each other. This can lead to occlusions and even collisions happening during occlusions. This scenario can be thought of as adding a third dimension where the size indicates the distance to the observer on the z-axis and each circle moves in a 2D plane with no velocity in z-direction.
A Box of Protons: Introducing Long-Range Interactions
Our main finding from conducting experiments with the above two datasets (and further variations) was that the instances where relational reasoning was necessary were too sparse. We hence introduced long-range interactions. This means that in order to predict the next time step accurately, the model has to take the forces from the other particles into account. Each circle can be thought of as a proton. Hence, all circle repell each other with that scales as $1/r$ with $r$ being the distance.
Protons and Electrons
Suprisingly, HART, our baseline object-tracker without relational reasoning, was still able to predict future locations with very high accuracy. The reason being the following: As the scenario is fully deterministic, the model can infer the force field from just the motion of a single particle. We hence further increased the difficulty with two more modifications.
In a first step, we added electrons, yielding two different, colour-coded identities and two types of interactions. Different charges attract each other and same charges repell each other. We changed the scaling of the force to $1/\sqrt(r)$ to avoid one dominant interaction per particle. Furthermore, we increased the maximum force value making the behaviour more ‘jumpy’. Due to having both attracting and repulsive forces, this scenario is prone to create scenarios where the particles are stuck (either in corners or on each other). To counter this, the simulation algorithm detects stuck particles and reassigns their identities.
In a second step, we introduced an additional hyperparameter randomness with values between 0 and 1. This parameter determines the likelihood with which a particle in a specific time step gets reassigned their identity. This now adds a high level of stochasticity to the scenarios. Accurately inferring the forces acting on a particular particle in a given time step should only be possible by taking information about other particles in this time step into account.
Protons and Electrons: Evaluation
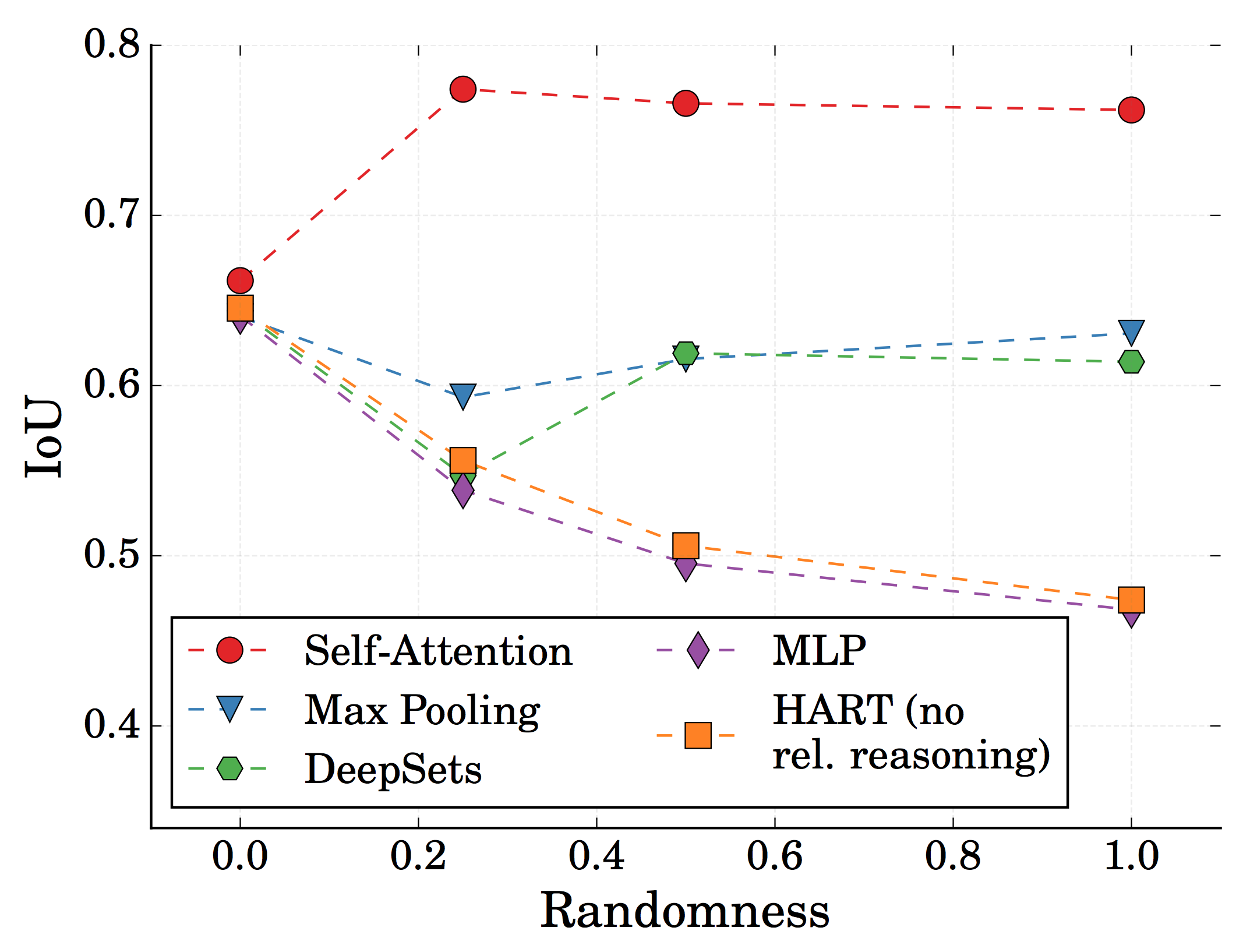
The following figure shows the quantitative results of MOHART on the proton-electron toy experiments. The x-axis represents the randomness, i.e. the likelihood of identitity-reassignment in each time step. The y-axis shows intersection of union of the predicted vs. ground truth bounding boxes one time step into the future. For the baseline without relational reasoning, we applied HART, an end-to-end single object tracker for each object in parallel. The other models are different versions of MOHART, which differ by the way relational reasoning is implemented, i.e. how information is exchanged between the different object trackers. For a detailed interpretation of the results, we refer the reader to the paper.
Conclusion
We provide a collection of physics-inspired toy datasets for testing tracking and relational reasoning performance. We found it suprising and insightful to realise how difficult it was to create a dataset which properly tests the relational reasoning capabilities of a model in a short-horizon trajectory prediction task. In order to achieve this, we needed to include both long-range interactions as well as stochasticity. Only the comnbination of the two rendered the problem sufficiently non-deterministic from the perspective of a single-object tracker to create a significant performance delta between single-object and multi-object tracking / trajectory prediction.
Download Data
Get the data + readme from here.
Paper
Find the paper here.
Credit: I conducted this work at A2I (Oxford University), supervised by Ingmar Posner and in collaboration with Adam Kosiorek, Oiwi Parker Jones and Kevin Li.