Equilibrium Aggregation

April 2022

---

In this post, we¹ will look at a core building block of many graph neural networks: permutation invariant aggregation functions. We start with a general introduction, motivating why this is an important topic, and then introduce a new form of aggregation, using an implicit layer: Equilibrium Aggregation. This is a stand-alone post, but it also reads well as a follow-up post to this one about learning on different neural network architectures for set-based problems, especially if you are not very familiar with the concept of permutation invariance.

Let’s dive right into it: a graph neural network that predicts a global property (typically either performing regression or classification) usually consists of multiple message passing layers followed by a global pooling layer followed by a fully connected block:

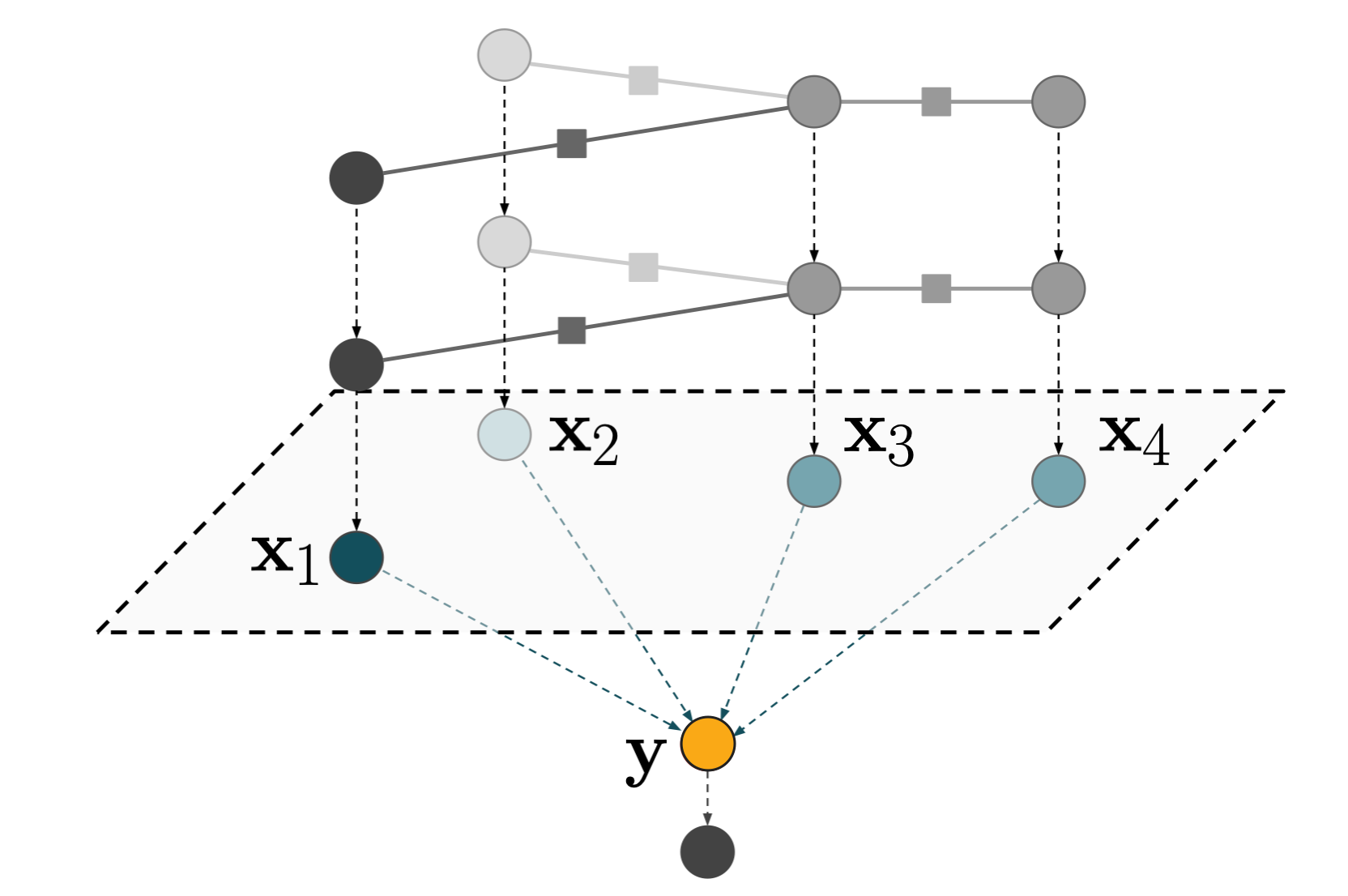
Let’s have a closer look at the pooling layer, i.e. the mapping from green -> orange in the figure above. The inputs to that pooling layer are node embeddings $\mathbf{x}_i$ and the output is a single (global) embedding $\mathbf{y}$. This is a particularly interesting point of the graph neural network for two reasons:

• This task of aggregating a set of (node) embeddings into a single embedding features an important symmetry, namely permutation invariance. In other words, there is no intrinsic ordering of the nodes and which of the nodes we label as $x_1$ (vs. $x_2$ etc.) is arbitrary.
• The number of activations suddenly drops from $N \times \text{embedding size}$ to $1\times \text{embedding size}$. This is often a bigger change than anywhere else in the network. We showed previously that this can introduce a bottleneck for the information flow (Wagstaff et al. 2020, Wagstaff et al. 2022).

The former point implies that, if we want to exploit this symmetry, we are massively restricted in the types of neural network layers we can apply. Luckily, because most people ignore edge information and solely use node information at this point, we can leverage our knowledge from the set learning literature to understand what the options are at this point.

In Review: Deep Learning on Sets, we found that most deep learning models that operate on sets belong to the permuting & averaging paradigm. Specifically, almost all of them can be seen as variants of Janossy pooling with $k=1$ (Deep Sets, PNA) or $k=2$ (Self-Attention), which we visualised as follows:

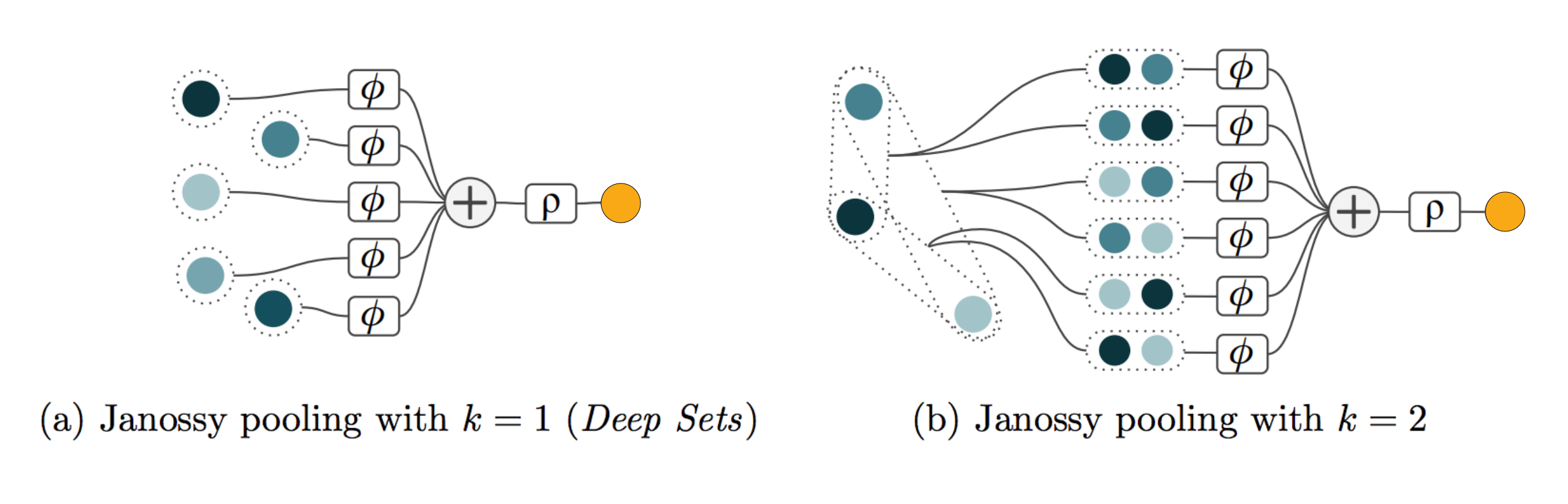
where $\phi$ and $\rho$ can be arbitrary neural networks². Realising the overwhelming dominance of these two flavours in the literature³ raises an obvious question: have we found the global optimum of how to do global aggregation or are we stuck in a local minimum?

Interestingly, all the architectures we covered in the previous blog post are explicit layers. Concretely, the output of these layers can be written as a closed-form mathematical expression. This misses an entire subfield of deep learning: implicit layers – for instance Deep Equilibrium Models, or Neural ODEs. The idea of implicit layers is defining conditions which the output has to satisfy. In Deep Equilibrium Models, the output is the fixpoint of a function that is conditioned on the input. In Neural ODEs, the output is the solution of a differential equation (evaluated at a certain time step into the future).

In Equilibrium Aggregation, we propose such an implicit layer for global aggregation. We define the output of the layer as the argmin of an energy function conditioned on the inputs (i.e. the node embeddings). The energy function has two key properties:

• It is permutation invariant w.r.t. the ordering of the input embeddings.
• It is parameterised by a neural network.

We choose the energy $E_{\theta}$ to be the sum of pairwise potentials $F_{\theta}(\mathbf{x}_i, \mathbf{y})$ with an additional regulariser term $R(\mathbf{y})$. Mathematically, the aggregation layer is defined as follows:

\[\phi_{\theta}(X) = \arg \min_{\mathbf{y}} E_{\theta}(X, \mathbf{y}) \\ E_{\theta}(X, \mathbf{y}) = R(\mathbf{y}) + \sum_{i=1}^N F_{\theta}(\mathbf{x}_i, \mathbf{y})\]

where the subscript $\theta$ inidicates that the pairwise potential $F$ is parameterized by a neural network. Because we solve the minimisation problem by doing gradient descent, the network weights $\theta$ will be updated through gradients of gradients. In theory, the regularizer could also be implemented as a neural network, but we simply choose it to be:

\[R(\mathbf{y}) = \text{softplus}(\lambda) \cdot || \mathbf{y} ||_2^2\]

to encourage convexity of the energy $E$ with respect to $\mathbf{y}$. Interestingly, depending on what forms the (learned) pairwise potential takes, this can recover many of the classic aggregation functions. In fact, when allowing $\mathbf{y}$ to be a vector in $\mathbb{R}^N$ where $N$ is the number of inputs, we prove that all possible permutation invariant, continuous functions can be learned. The following table shows the pairwise potential functions $F$ that the network would have to learn in order to recover mean pooling, max pooling, sum pooling or median pooling:

Interestingly, sum and max pooling can be represented⁴ by equilibrium aggregation with just one latent dimension (i.e. $\mathbf{y} \in \mathbb{R}^1$). In contrast, one latent dimension is provably not enough to represent sum pooling via max pooling and vise versa.

We provide empirical evidence for this flexibility, too. In a toy experiment on median estimation, equilibrium aggregation outperforms sum-aggregation and multi-head attention by 1, sometimes 2 orders of magnitude. Going beyond toy problems, in the established MOLPCBA benchmark for example, swapping out explicit layer aggregation functions with Equilibrium Aggregation also gives consistent performance improvements.

So far, we have been focussing on global graph aggregation. However, graph neural networks have additional places where permutation invariant aggregation is performed: when passing messages from edges to nodes. Often, a message to a node is computed as the sum over all the incoming edges: \(m_i = \sum_{j\,\in\,\mathcal{N}_i} e_{ij}\)

Equilibrium Aggregation can be applied in this scenario, too. In fact, we do so in one of our experiments, yielding slight improvements. This was not the main focus of the paper, and likely there would be some tricks to make this work even better.

The message passing application scenario of Equilibrium Aggregation has interesting parallels with a concurrently developed approach, the Constraint-Based Graph Network Simulator. In Equilibrium Aggregation, we optimize one global $\mathbf{y}$, and the optimization is performed for a specific layer of the network. In contrast, Rubanova et al. optimize $\mathbf{y}_i$ for each graph node, where $\mathbf{y}_i$ is an input to the entire network. This approach can be thought of as optimizing the nodes to satisfy learned constraints. This is a smart way of adding a helpful inductive bias to the network, for example when the task is to simulate/predict the future of a physical system. In this case, learning a constraint that leads to accurate predictions can be seen as tantamount to capturing the dynamics and physical rules of the system. If you find the Equilibrium Aggregation approach interesting, definitely check out their work, too.

So, what’s next? We are hoping that someone will take this idea (code is in the appendix of the paper) and try it out in SOTA graph net approaches. Current SOTA approaches tend to be more finetuned and might require additional tuning & tricks (or maybe not?) to explore the full potential of Equilibirum Aggregation. If you do, please let us know how it worked out for you. Other ideas for future work include further exploring the node level aggregation approach, or going from Janossy pooling with $k=1$ (what we are doing now) to $k=2$ (self-attention ftw).