Learning Invariant Representations
Credit: I conducted this work at A2I (Oxford University), supervised by Ingmar Posner and in collaboration with Adam Kosiorek, Alex Bewley, Andrea Vedaldi, Daniel Worrall, Edward Wagstaff, Li Sun, Martin Engelcke, Markus Wulfmeier, Max Welling, Michael Osborne, Oiwi Parker Jones, Oliver Groth, Volker Fischer. I would like to thank the EPSRC as well as Kellogg College Oxford for funding.
Introduction
In machine learning, models need to learn to ignore unimportant or even distracting features. These are typically features that correlate with target labels in the training data - but not the test data. Generalisation is, after all, the goal of most machine learning algorithms. It requires a trade-off between
-
sensitivity to relevant features in the data and
-
methods to suppress distractions
My research addresses the second point. More specifically, it focusses on ways of directly modelling invariance so as to suppress unimportant or distracting features and improve overall performance.
The most wide-spread way of suppressing noisy features in the input is regularisation, which aims at mitigating overfitting. Examples include weight decay, early stopping or dropout. These techniques share the underlying principle of Occam’s razor, which is indispensable in machine learning and key for good generalisation. However, I’d like to focus on more targeted forms of invariances.
In the following, I will explain my work published on this topic to date. It divides into two sub-topics. First, I will introduce neural stethoscopes, which, among other things, enable suppression of features if they are connected to a label which comes with the dataset (or can be easily obtained e.g. using a pre-trained classifier). Second, I will go into permutation invariance, where we seek to create representations which are invariant with respect to the order of the input. I will explain why these cases profit from explicitly using permutation invariant architectures. I will provide both theoretical and practical evidence of the usefulness of this type of architecture.
Ignoring a Specific Feature: De-Biasing
In this section, we look at classification scenarios where an additional label for each (or some of the) data points are available. We might not know beforehand whether this additional label
- represents a nuisance factor, in which case we can use it to de-biase the model by enforcing invariance
- is beneficial for the learning process, in which case we might want to use it as an auxiliary loss
In Scrutinizing and De-Biasing Intuitive Physics with Neural Stethoscopes, we propose the concept of neural stethoscopes. It unifies existing work on interpretability, auxiliary, and adversarial learning. Neural stethoscopes are a straight forward extension of multi-task learning. However, with existing auxiliary and adversarial learning techniques, practitioners hypothesise beforehand whether it is helpful for the network to learn a second task in parallel (auxiliary training, e.g. Mirowski et al.) or whether the second label represents a harmful nuisance factor which should be suppressed (e.g. Louizos et al.).
The following figure illustrates an example of a neural stethoscope (orange) attached a hidden layer of the main network (blue). We investigate the efficacy of this approach in the context of stability prediction of block towers, a popular task in the domain of intuitive physics. Note that enc (encoder) and dec (decoder) does not imply that this needs to be an autoencoder structure, it could be any network (in our case it was Inception-v4). The main network is trained on the main task (here: global stability), whereas the stethoscope is trained on a secondary task (here: local stability).
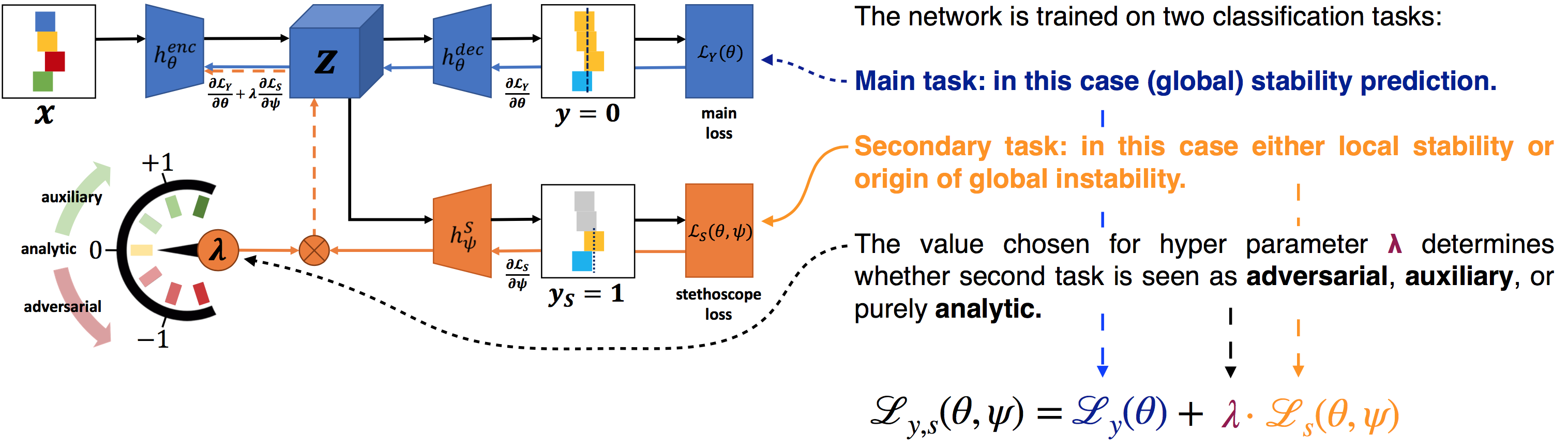
The loss from the secondary label is back-propagated as normal into the stethoscope (orange). Crucially, the encoder part of the main network is also updated according to the stethoscope loss, but whilst applying a pre-factor $\lambda$. Positive values for $\lambda$ correspond to traditional auxiliary learning whereas negative values lead to a min-max game (similar to GANs) between stethoscope and main network leading to suppression of features which correlate with the secondary label. Setting this hyperparameter to 0 leads to no gradient updates in the main network. This is the analytic mode of the stethoscope which for example allows for layer-to-layer comparison of how much (disentangled) information there is in each layer of the network with respect to a specific task.
Ignoring Order: Permutation Invariance
Second, we look at scenarios where we seek invariance with respect to an aspect of the input structure as opposed to a specific feature. Specifically, we look at set-based problems. Sets are sequences of items, where the ordering of items carries no information for the task in hand. An example is anomaly detection. E.g., Lee et al. train a neural net on detecting outliers from a set of images as shown below:

Obviously, in this case, we do not want the model to care about the order of which these images are presented in. Hence, we want the model to permutation invariant with respect to its inputs.
To give an intuitive mathematical explanation for permutation invariance, this is what a permutation invariant function with three inputs would look like:
$f(a, b, c) = f(a, c, b) = f(b, a, c) = \dots$
Some other practical examples where we want to treat data or different pieces of higher-order information as sets (i.e. where we want permutation invariance) are:
- working with sets of objects in a scene (think AIR or SQAIR)
- multi-agent reinforcement learning
- perhaps surprisingly, point clouds
Permutation Invariance and Universal Function Approximation
Having established that there is a need for permutation-invariant neural networks, let’s see how to enforce permutation invariance in practice. One approach is to make use of some operation $P$ which is already known to be permutation-invariant. We map each of our inputs separately to some latent representation and apply our $P$ to the set of latents to obtain a latent representation of the set as a whole. $P$ destroys the ordering information, leaving the overall model permutation invariant.
In particular, Deep Sets does this by setting $P$ to be summation in the latent space. Other operations are used as well, e.g. elementwise max. We call the case where the sum is used sum-decomposition via the latent space. The high-level description of the full architecture is now reasonably straightforward - transform your inputs into some latent space, destroy the ordering information in the latent space by applying the sum, and then transform from the latent space to the final output. This is illustrated in the following figure:
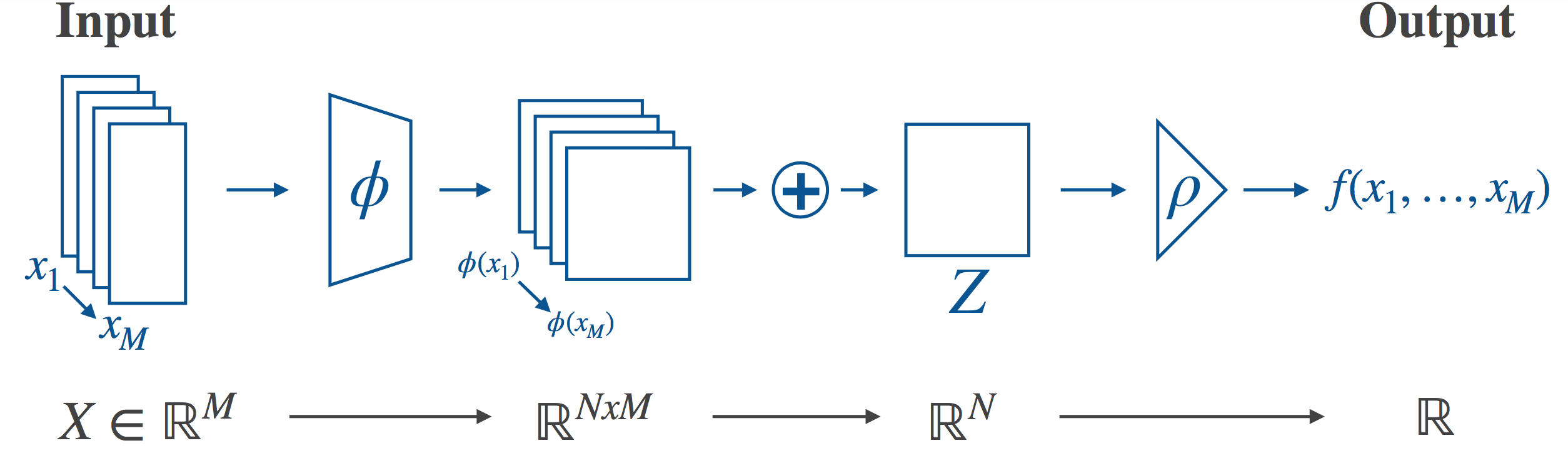
If we want to actually implement this architecture, we will need to choose our latent space (in the guts of the model this will mean something like choosing the size of the output layer of a neural network). As it turns out, the choice of latent space will place a limit on how expressive the model is. In general, neural networks are universal function approximators (in the limit), and we’d like to preserve this property. Zaheer et al. provide a theoretical analysis of the ability of this architecture to represent arbitrary functions - that is, can the architecture, in theory, achieve exact equality with any target function, allowing us to use e.g. neural networks to approximate the necessary mappings? In our paper (On the Limitations of Representing Functions on Sets), we build on and extend this analysis, and discuss what implications it has for the choice of latent space.
Permutation Invariance and Relational Reasoning
Let’s look at a practical application of our acquired understanding of permutation invariant architectures: relational reasoning $-$ the ability to model interactions and relations between objects. A machine learning model performing relational reasoning often has access to a list of object representations. The ordering of the list could carry information for the task at hand, but that is not necessarily the case. Often, relational reasoning calls for permutation invariant (or equivariant) architectures. In End-to-end Recurrent Multi-Object Tracking and Trajectory Prediction with Relational Reasoning, we examine the importance of relational reasoning and the role of permutation invariance in a real-world setting.
To do so, we build on Hierarchical Attentive Recurrent Tracking (HART), a recently-proposed single-object tracker trained fully end-to-end. Contrary to tracking-by-detection, where only one video frame is typically processed at any given time to generate bounding box proposals, end-to-end learning in HART allows for discovering complex visual and spatio-temporal patterns in videos, which is conducive to inferring what an object is and how it moves. In the original formulation, HART is limited to the single-object modality. We augment HART to tracking multiple objects simultaneously in a way that enables the model to perform relational reasoning. This can be helpful, e.g., to avoid performance loss under self-occlusions of tracked objects or strong camera motion.

The figure above shows a sketch of the MOHART architecture. A glimpse is extracted for each object using a (fully differentiable) spatial attention mechanism. These glimpses are further processed with a CNN and fed into a relational reasoning module. A recurrent module which iterates over time steps allows for capturing of complex motion patterns. It also outputs spatial attention parameters and a feature vector per object for the relational reasoning module. Dashed lines indicate temporal connections (from time step $t$ to $t+1$).
The entire pipeline operates in parallel for the different objects, only the relational reasoning module allows for the exchange of information between tracking states of each object. We argue that this is a set-based problem: the ordering of the list of object representations carries no meaning for the task at hand. A naive way of introducing meaning to the order would be to leverage location information, which of course is highly relevant for relational reasoning. However, location information is two dimensional whereas a list is one dimensional and carries no information about distance. Hence, we argue that it is much more beneficial to include positional encoding into the object representations and use a permutation invariant architecture. We show that processing the information in a non-permutation manner shows no performance improvement compared to single object tracking (i.e. no relational reasoning), despite being theoretically capable of learning permutation invariance and having more capacity. We further show that, in this setting, the DeepSets architecture, which has been widely used and studied in the context of set-based problems, despite theoretically allowing for universal approximation of all permutation invariant functions, is inferior to multi-headed self-attention. On three real-world datasets, we show consistent performance improvements of MOHART compared to HART.